Relatività. È il 1905 quando un anonimo 26 enne che lavora all’ufficio brevetti di Berna pubblica l’opera che avrebbe rivoluzionato la fisica teorica e il modo in cui l’uomo avrebbe guardato la realtà. Il suo nome era Albert Einstein
Da sempre ambiamo a comprendere la natura dei fenomeni che ci circondano, di definirli, di prevederli o addirittura di controllarli. Ma questa umanissima ambizione si scontra con le modestissime risorse di cui disponiamo.
La nostra mente, come quella di qualsiasi altro animale, mette insieme l’enorme mole di dati che provengono dagli organi di senso per ricostruire una rappresentazione della realtà. Viene quindi da chiedersi quanto sia veritiera questa proiezione mentale e quanto di illusorio ci sia nel mondo in cui siamo abituati a vivere.
È ironico pensare che sempre nel nostro intelletto ci sia la potenzialità di trascendere il nostro umano punto di vista per assumere, magari per un momento, una prospettiva assoluta sull’assoluto. È così che le più grandi scoperte sono state fatte; grazie a intuizioni ardite che hanno scardinato le modalità in cui da sempre siamo stati abituati a pensare la realtà, tanto nel nostro vivere quotidiano quanto nel mondo della fisica. Ed è proprio di un’intuizione ardita, di una teoria irriverente che oggi parleremo: la teoria della relatività ristretta.
“Relatività: tempo e spazio”
– N. 1
Questo è il primo numero della Rubrica di Area dal titolo “Relatività: tempo e spazio”, appartenente alla Macroarea di Scienze
Il tempo assoluto
Una delle nostre più monolitiche certezze, delle fondamenta del nostro pensare l’universo è stato il tempo. Sin dall’antichità sulla definizione e sulla natura del tempo ci si è interrogati, forse in ragione anche del suo intimissimo rapporto con il concetto di caducità e mortalità.
Una delle concezioni più umanamente accettabili sulla natura del tempo ci è stata offerta da Aristotele.
Il tempo è il numero del movimento secondo il prima e il poi
E dato che il movimento è eterno anche il tempo lo è. In altri termini il tempo sarebbe la misura di un movimento o, se vogliamo, di un mutamento.
Nella fisica, invece, il tempo è un parametro matematico usato per descrivere il movimento dei corpi nello spazio. Nella Fisica classica questo parametro t è assoluto, uguale a sé stesso in ogni punto dell’universo, in ogni sistema di riferimento. Possiamo dire, quindi, che anche nella nostra esperienza quotidiana il tempo è una costante; per quanto la nostra percezione psicologica del tempo sia variabile, un’ora è sempre composta da 60 minuti e come tale la sua durata non cambia.
Nei primi anni del ‘900 questa convinzione fu completamente ribaltata per risolvere una delle grandi crisi che la fisica ha dovuto affrontare. Parliamo dello scontro della Meccanica Classica con le equazioni di Maxwell sull’elettromagnetismo.
Per capire l’entità del problema e la genialità dell’intuizione di Einstein nel risolvere questo conflitto apparentemente insanabile, ripercorreremo, una dopo l’altra, le tappe della teoria tra le più affascinanti della fisica teorica e sarà lo stesso Albert Einstein a guidarci, nel suo libro: Relatività. Esposizione divulgativa.
La relatività del moto
La fisica classica, i cui padri indiscussi furono Galileo Galilei e Isac Newton, si è occupata in primo luogo di movimento. Non è altro che la meccanica, forse la più odiata branca dagli studenti, è il punto di partenza della riflessione di Einstein.
Studiare il moto di un corpo significa cercare di definire come la sua posizione nello spazio cambi in funzione dello scorrere del tempo. Ma anche un compito apparentemente così modesto nasconde delle insidie. Proviamo a immaginare, suggerisce Einstein, di essere al finestrino di un treno in corsa di moto rettilineo uniforme (cioè un moto in cui la velocità rimane costante e la traiettoria descritta dal corpo in moto, il treno nel nostro esempio, sia una retta); poniamo di lasciar cadere una pietra dal finestrino senza imprimerle nessuna forza. Dal nostro punto di vista essa cadrà perpendicolarmente al terreno. Se, però, qualcun altro avesse guardato la scena stando seduto sulla banchina ci avrebbe restituito un’esperienza diversa. La pietra, infatti, avrebbe descritto una traiettoria parabolica e non più retta. Viene dunque da chiedersi: qual è la traiettoria reale descritta dalla pietra nello spazio?
Anzitutto, suggerisce Einstein, eliminiamo la parola spazio che di per sé è molto vaga e non ci dice granché. Al suo posto usiamo un sistema di riferimento rigido rispetto al quale riferire il moto che possiamo definire sistema di coordinate. Il moto della pietra descrive, dunque, rispetto a un sistema di coordinate solidale al vagone una traiettoria retta e rispetto a un sistema solidale alla banchina una traiettoria parabolica.
In definitiva il moto di un corpo dipende dal sistema di coordinate dal quale è osservato.
Il principio della relatività ristretta di Galilei
Ben presto Galilei si accorse che le leggi della meccanica sono valide per tutti i sistemi di coordinate che si muovono in moto rettilineo uniforme l’uno rispetto all’altro (principio di relatività Galileiana).
Proviamo ad immaginarci dentro la cambusa di una nave che si muove di moto rettilineo uniforme; secondo Galilei nessun fenomeno meccanico potrebbe farci capire se la nave è ferma o in navigazione. Nulla si muove nella direzione opposta al movimento perché non essendoci accelerazione non c’è neppure quella forza fittizia che è l’inerzia.
Per lungo tempo si credette che tutti i fenomeni della fisica potessero essere coerenti con il principio di relatività galileiano; ma nell’800, con gli studi sull’ottica e sull’elettromagnetismo, anche questo principio divenne maturo per essere messo in discussione.
Le leggi dell’elettromagnetismo, infatti, sembravano cambiare in funzione del sistema di riferimento preso in esame e questo le rendevano in aperto contrasto con il principio Galileiano.
Cosa fare, dunque? Rinnegare le nuove teorie, così incredibilmente adatte a spiegare e a prevedere gli esiti delle esperienze fatte su fenomeni elettromagnetici? Oppure smantellare il caposaldo della meccanica Galileiana e Newtoniana che era risuscito a spiegare la caduta dei gravi e di predire con una precisione miracolosa il moto dei corpi celesti?
I fisici tentarono, quindi, per tener salve le due teorie, di ipotizzare l’esistenza di una sostanza che permeasse tutto l’universo che chiamarono etere luminifero, o semplicemente etere. Questa sostanza, dalle proprietà molto singolari, avrebbe rappresentato un sistema di riferimento privilegiato, considerabile perfettamente in quiete, rispetto al quale le leggi dell’elettromagnetismo potessero venire formulate in modo particolarmente semplice.
Per tutti gli altri sistemi di riferimento, in moto rispetto all’etere, le leggi avrebbero perso quella semplicità per il semplice fatto di dover includere degli altri parametri, come la velocità o la direzione del moto del sistema di riferimento in questione.
L’addizione delle velocità secondo la relatività galileiana
Una delle fondamenta della meccanica classica è il teorema di addizione delle velocità, tanto semplice quanto irrinunciabile per la sua innegabile evidenza.
Per capirlo torniamo ancora in stazione, tanto amata da Einstein. Immaginiamo di essere noi, ad essere seduti sulla banchina e di osservare un uomo in un treno che si muove a velocità costante v in linea retta; ipotizziamo poi che l’uomo stia camminando dentro il vagone nella stessa direzione di marcia del treno con una velocità w. A quale velocità si muoverebbe il passeggero rispetto alla banchina? Appare evidente che la velocità effettiva dell’uomo risulterebbe essere pari alla somma della sua velocità con quella del treno: w + v.
Immaginiamo, quindi di ripetere l’esperimento, ma anziché osservare un uomo camminare dentro il vagone, immaginiamo di vedere un raggio di luce sfrecciare alla velocità c. In analogia al caso precedente, saremmo portati a considerare la velocità con cui si allontana il raggio di luce da noi pari a c + v. Tuttavia, questo non è possibile secondo la legge di propagazione della luce nel vuoto per la quale la velocità della luce c è costante e pari a circa 300.000 km/s.
Il principio di relatività galileiano e la legge di propagazione della luce nel vuoto sono in disaccordo; l’innegabile ragionevolezza del principio di galilei ci indurrebbe a scartare la teoria della costanza della velocità della luce, ma gli esiti successivi della fisica teorica e soprattutto delle esperienze hanno confermato la validità di quest’ultimo postulato: c è una costante e rappresenta un limite irraggiungibile e invalicabile per qualunque corpo dotato di massa.
A questo punto entrò in gioco la relatività ristretta o speciale, così detta perché risolse il conflitto fra meccanica ed elettromagnetismo limitandosi alla trattazione di moti inerziali, cioè in moto rettilineo uniforme gli uni rispetto agli altri.
Tempo e Spazio relativi o assoluti?
L’incompatibilità tra il principio di propagazione della luce nel vuoto e il principio di relatività si basa su due ipotesi gratuite della meccanica classica:
- L’intervallo di tempo tra due eventi è indipendente dalle condizioni di moto del corpo di riferimento;
- L’intervallo di spazio fra due punti in un corpo rigido è indipendente dalle condizioni di moto del corpo di riferimento.
In altri termini, la fisica classica ha sempre implicitamente presupposto l’assolutezza del tempo e dello spazio, come d’altronde i nostri sensi ci spingerebbero a credere. E se così non fosse?
Beh, se questi presupposti fossero sbagliati, la contraddizione tra relatività e costanza della velocità della luce cesserebbe di esistere; il teorema della somma delle velocità non sarebbe più applicabile dato che i due parametri di spazio e tempo, che definiscono la velocità, sono relativi e non uguali in tutti i sistemi di riferimento.
Le trasformazioni di Lorentz
Fino ad ora abbiamo considerato luoghi e tempi rispetto al treno e rispetto alla banchina. In che modo possiamo trovare il tempo e il luogo di un evento sul treno quando ne conosciamo il luogo e il tempo secondo la banchina? Si può dare una risposta a questa domanda tale che la velocità della luce rimanga costante rispetto ad entrambi i sistemi di coordinate?
La risposta è nettamente affermativa ed è stata data dalle trasformazioni di Lorentz. Generalizziamo i nostri sistemi di riferimento consueti (la banchina e il treno) riferendoci ad essi con le lettere K e K’ e rappresentiamoli ciascuno come un sistema di coordinate spaziali e temporali: x, y, z e t per il sistema K e x’, y’, z’ e t’ per il sistema K’.
Conoscendo le coordinate dell’evento rispetto a K (la banchina) possiamo calcolare le coordinate dell’evento rispetto a K’ con le seguenti equazioni:
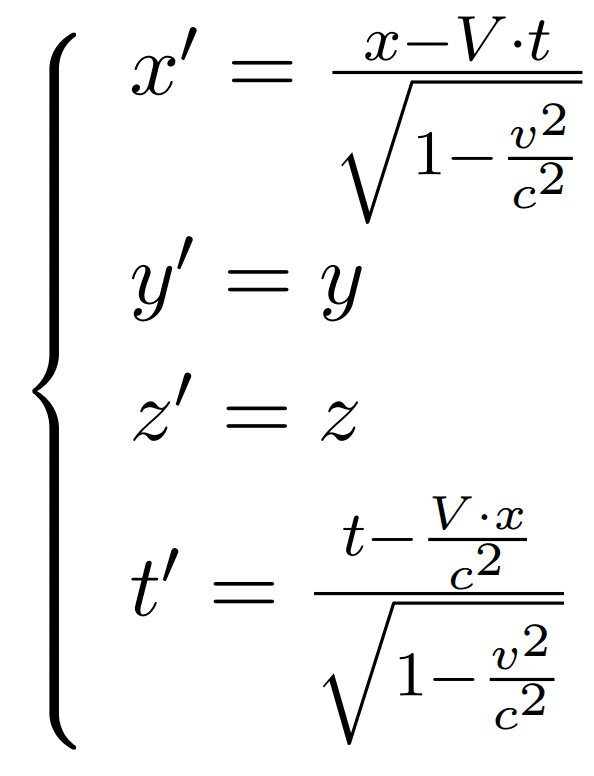
Immaginiamo di lanciare un segnale luminoso lungo l’asse positivo delle ascisse. La posizione raggiunta (x) nel tempo (t) dal fascio di luce sarà pari a ct. Sostituendo a x, ct nelle trasformazioni di Lorentz e risolvendole si otterrà che sia per il sistema di riferimento in quiete che per quello in moto la c è la stessa e pari a 300.000 km/s. Il conflitto è risolto.
Le implicazioni fisiche di queste apparentemente sterili equazioni matematiche sono tra le più controintuitive della fisica teorica… ma necessitano di tempo per essere raccontate.
Francesco Lodoli per Questione Civile
Bibliografia
Relatività. Esposizione divulgativa e scritti classici su Spazio Geometria Fisica


