La relatività di spazio e tempo: dalle trasformazioni di Galilei a quelle di Lorentz
Stiamo per entrare finalmente nel vivo della relatività ristretta, nell’Universo Immaginato da Einstein, tanto bizzarro quanto affascinante. Ma affinché quanto verrà descritto di questo nuovo fantastico Mondo non venga creduto per fede o per semplice riverenza nei confronti di una delle menti più illuminate del Novecento, è necessario al lettore un piccolo sforzo intellettuale, sopportando pochi semplici passaggi matematici che richiedono solo, e ce lo dice anche Einstein, la licenza liceale. Se avrete la voglia e la curiosità di farlo, sarete voi stessi a tirare le somme dalle premesse di Einstein, intuendo delle verità sulla nostra realtà che sono precluse ai nostri sensi, e che sembrano ribellarsi a tutto quanto c’è di sensato nella nostra percezione quotidiana del mondo. Riprendiamo il nostro discorso da dove lo avevamo lasciato, facendo però un piccolo passo indietro.
“Relatività: tempo e spazio”
– N. 2
Questo è il secondo numero della Rubrica di Area dal titolo “Relatività: tempo e spazio”, appartenente alla Macroarea di Scienze
La relatività di Galilei
Il principio di relatività galileiana afferma che le leggi della meccanica sono covarianti per sistemi di riferimento inerziali, cioè in moto rettilineo uniforme l’uno rispetto all’altro (vd. il primo articolo della rubrica se non lo hai ancora fatto!). Detto in termini più semplici, ogni legge della meccanica, come la famosa formula F = ma, è la stessa per qualunque sistema di coordinate inerziale (in moto a v = costante).
Galilei, quindi, crea delle formule – dette trasformazioni di Galilei-Newton – che permettono di descrivere le coordinate spazio-temporali di un evento rispetto a qualsiasi sistema di riferimento in moto rettilineo uniforme rispetto a un altro.
Le trasformazioni galileiane
Riprendiamo l’esempio della stazione: immaginiamo di trovarci sulla banchina in un punto che idealmente facciamo coincidere con l’origine di una terna di assi cartesiani (x,y,z) che definiamo S (sistema di riferimento in quiete rispetto al treno); e immaginiamo che un nostro caro amico si trovi al finestrino di un treno e incrociamo il suo sguardo in un istante di tempo iniziale che chiamiamo t0. Il nostro amico sarà a una distanza x’ dall’origine della terna di assi cartesiane (x’, y’, z’) del sistema di riferimento S’, in moto rettilineo uniforme rispetto alla banchina.
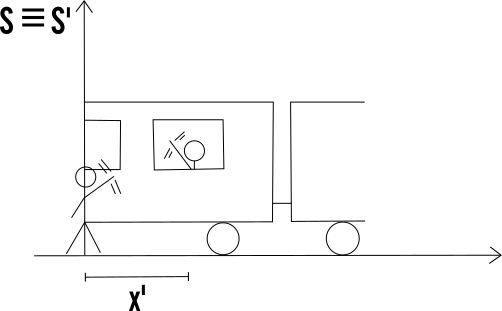
Nell’istante di tempo t1, il treno sarà traslato in avanti lungo l’asse delle ascisse di una certa distanza x0 che è pari al prodotto fra la sua velocità e il tempo trascorso (vt). Come possiamo quindi calcolare la posizione del nostro amico in relazione al nostro sistema di riferimento in quiete S (la banchina)?
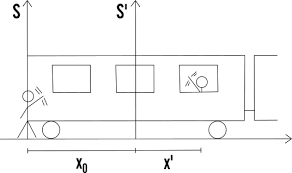
x = x’ + x0 à ma x0 è uguale a vt; quindi, x = x’ + vt à per trovare x’ basta portare vt al primo membro: x’ = x – vt.
Essendo il movimento traslatorio sull’asse delle x, la posizione del nostro amico secondo le altre coordinate spaziali rimarrà invariata:
y = y’
z = z’
Il tempo per Galilei è assoluto, cioè scorre sempre alla stessa velocità per tutti gli osservatori, quindi:
t = t’.
Quelle che abbiamo descritto sono le celebri trasformazioni di Galilei.
L’invarianza delle lunghezze
Seguitemi ancora in queste banali considerazioni:
immaginiamo che sul sistema di riferimento in moto sia posizionato sull’asse delle ascisse un regolo rigido di una certa lunghezza l’. Ovviamente la lunghezza del regolo potrà essere descritta come quella di un segmento avente come estremi due punti sull’asse delle ascisse: x’1, x’2.
Possiamo definire, quindi, l’ come la differenza tra x’2 e x’1. Usando le trasformazioni di Galilei:
l’ = x’2 – x’1 = (x2 – vt) – (x1 – vt) = x2 – x1 = l (cioè la lunghezza del regolo nel sistema di riferimento in quiete)
Da questi semplici passaggi matematici si arriva alla conclusione, piuttosto intuitiva e scontata, che no, la lunghezza del regolo non cambia, neppure se si trova in un sistema di riferimento in moto. La lunghezza di un corpo rigido è dunque invariante rispetto alle trasformazioni di Galilei, cioè il suo valore è costante indipendentemente dal sistema di riferimento indagato.
Applicando le trasformazioni di Galilei ed eseguendo qualche passaggio matematico è possibile verificare la legge della composizione delle velocità (vi rimando, ancora, al primo articolo di rubrica), oppure la covarianza di celebri leggi della meccanica, o l’invarianza di alcune grandezze come l’accelerazione.
Allora perché introdurre le trasformazioni di Lorentz, ben più bizzarre e complicate di quelle di Galileo? Per comprendere meglio una nuova branca della fisica: quella dell’ottica e dell’elettromagnetismo. La relatività galileiana, infatti, funzionava benissimo per studiare la caduta dei gravi e il moto dei corpi celesti, ma non era sufficiente a descrivere efficacemente il moto a velocità ben più elevate, come quella della luce.
Le trasformazioni di Lorentz
Per ricavare le sue trasformazioni, Lorentz è partito dall’assunto, che ha desunto dalle leggi dell’elettromagnetismo di Maxwell e dalle evidenze sperimentali, che la luce viaggia a velocità costante e pari a circa 300.000 km/s. Ha immaginato una sorgente luminosa posizionata all’origine degli assi del sistema di riferimento in moto e ha cercato di descrivere il moto della luce come un fronte d’onda sferica, giacché la luce è una radiazione isotropa, che si propaga in ogni direzione nello spazio.
Partendo da questo assunto (c = costante), Lorentz è pervenuto alle trasformazioni che abbiamo già introdotto nel primo articolo e la cui dimostrazione per il momento tralasciamo.
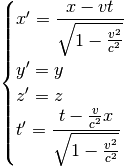
La cosa che attira subito la nostra attenzione di queste equazioni è x’: questa è del tutto simile alla equazione galileiana ma viene aggiunto un denominatore che possiamo anche definire, in modo più sintetico ed elegante, come fattore γ.
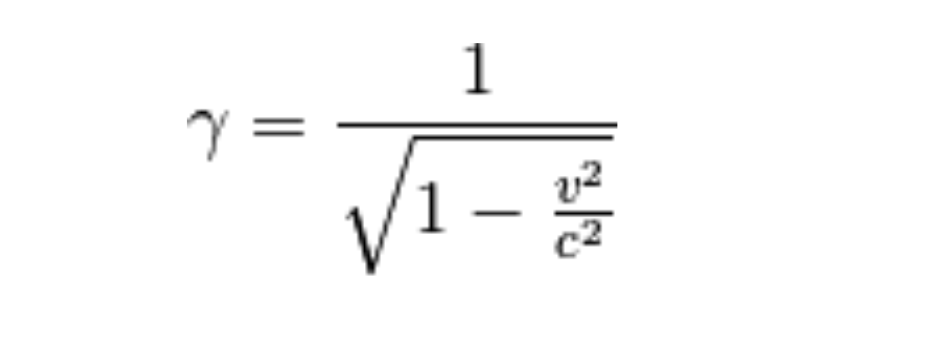
Giacché la velocità raggiunta dal sistema di riferimento (v) è sempre inferiore rispetto a c (per assunto), il rapporto tra v e c sarà sempre un valore compreso tra 0 e 1. Quindi il fattore γ (il rapporto di 1 e un numero compreso tra 0 e 1) sarà maggiore di 1; e sarà tanto maggiore quanto più la velocità v sarà vicina a quella della luce (c). Se non siete convinti di quanto ho detto, provate a sostituire alle lettere dei valori numerici arbitrari, purché il rapporto v su c sia una frazione impropria, cioè con numeratore minore in senso stretto rispetto al denominatore.
Dalle trasformazioni di Lorentz alla relatività: la contrazione delle lunghezze
Proviamo ora a calcolare la lunghezza del regolo rigido di prima l usando le trasformazioni di Lorentz, dove l’ è la lunghezza del regolo in quiete e l è la lunghezza dello stesso regolo in moto.
l’ = x’2 — x’1 = γ(x2 — vt2) — γ(x1 — vt1) = γ(x2 — x1) = γl
Seguendo questi semplici passaggi matematici si arriva alla conclusione che la lunghezza del regolo cambia con il moto: questa è diminuita rispetto alla lunghezza dello stesso regolo in quiete di un fattore γ. Einstein interpreta fisicamente le trasformazioni di Lorentz e arriva alla formulazione della prima paradossale verità della relatività ristretta: la contrazione delle lunghezze nella direzione del moto.
Ovviamente di questa contrazione non siamo consapevoli nella vita quotidiana dove facciamo esperienza di un moto estremamente più lento di quello della luce, ma se potessimo accelerare un corpo a una velocità vicina a c noteremmo con stupore questo straordinario effetto della relatività ristretta.
Dalle trasformazioni di Lorentz alla relatività: la dilatazione dei tempi
Passiamo ora ai tempi. Immaginiamo di posizionare nell’origine del sistema K’ un orologio ed indichiamo con t0 il tempo iniziale e t1 il primo rintocco immediatamente successivo. L’intervallo t1-t0 sarà proprio uguale a un secondo. Applichiamo anche al tempo le trasformazioni di Lorentz:
〖t’〗_1-〖t^’〗_0= γ(t_1- v/c^2 x_1 )- γ(t_0-v/c^2 x_2 )
Svolgendo qualche calcolo si ottiene il rapporto
(t_1-t_0)/γ
Essendo come già detto γ maggiore di uno, il rapporto sopra scritto sarà inferiore dell’intervallo di tempo t’1 – t’0,cioè l’intervallo di tempo trascorso nel corpo in moto. Il tempo, fino ad allora considerato eterno e immutabile è qualcosa di estremamente variabile, andando incontro a un rallentamento che dipende direttamente dalla velocità del sistema di riferimento considerato. Se per assurdo noi potessimo inventare una macchina in grado di viaggiare alla velocità c, per un osservatore esterno il tempo scandito dal nostro orologio sarebbe del tutto fermo.
Di contro per noi, all’interno della nostra autovettura, il tempo in tutto il mondo si sarebbe fermato, mentre solo le lancette del nostro orologio sembrerebbero muoversi.
Se poi volessimo verificare che la velocità della luce fosse costante, indipendentemente dalla velocità del sistema di riferimento, potremmo farlo ricordandoci che le equazioni di Lorentz sono state desunte proprio da questo postulato. Lorentz ha così ridotto le trasformazioni galileiane a un caso particolare: quando infatti la velocità del sistema di riferimento è molto piccola rispetto a c il fattore γ può essere trascurato così da riottenere le equazioni di Galilei.
L’esempio del Muone
Ogni istante l’atmosfera terrestre viene penetrata dai raggi cosmici, particelle che vengono dall’Universo a grande velocità. Le interazioni tra queste radiazioni e le molecole d’aria danno vita a delle particelle subatomiche di varie caratteristiche, tra le quali anche i muoni.
I muoni sono particelle molto instabili che decadono in 2 microsecondi ( 2 milionesimi di secondo) ma che viaggiano a una velocità pari al 99.5% di quella della luce. Con questa velocità in 2 microsecondi dovrebbero esser in grado di percorrere una distanza di circa 600 m, ma in realtà riescono a raggiungere persino la superficie terrestre!
Questo fenomeno paradossale può venire spiegato efficacemente dalla teoria della relatività ristretta e ne rappresenta un’importante prova sperimentale. A quelle velocità la vita di un muone per un osservatore esterno sarà molto più lunga, anche di 20 volte, per effetto della dilatazione dei tempi, permettendogli di percorrere i diversi chilometri dell’atmosfera terreste. Inoltre, ipotizzando di assumere la prospettiva del muone, la distanza che separerebbe il punto in cui il muone ha avuto origine e la superficie terrestre si sarebbe notevolmente accorciato, per la legge della contrazione delle lunghezze.
Francesco Lodoli per Questione Civile
Bibliografia
Relatività. Esposizione divulgativa e scritti classici su Spazio Geometria Fisica
Filosofia della Scienza. A cura di Giovanni Boniolo, B. Mondadori, Milano 1997
Le immagini appartengono ai legittimi proprietari. Utilizzo delle immagini divulgativo e non commerciale.


